자료구조 복습하기 #1리스트

1. 리스트의 추상 데이터 타입

<리스트>

리스트란 자료를 정리하는 방법 중 하나

*각 항목 간에 순서가 있는 집합과는 다르게 리스트는 각 항목 간에 순서가 지정되어있다.*

 

<리스트 ADT>

리스트 ADT란 리스트를 추상 데이터 타입으로 정의한 것

- 객체 -

n개의 element형으로 구성된 순서 있는 모임

- 연산 -

• insert(list, pos, item)
• delete(list, pos)
• clear(list)

등등

 

<리스트의 구현>

리스트는 배열과 연결 리스트로 구현할 수 있다.

	배열	연결리스트
장점	간편하고 속도가 빠르다	크기에 제한되지 않고, 유연한 리스트를 구현할 수 있다.
단점	리스트의 크기가 고정된다	구현이 복잡하고 임의의 항목을 추출하는데 시간이 걸린다.

 

2. 배열로 구성된 리스트

<배열 리스트의 정의>

#define MAX_LIST_SIZE 100 //리스트의 최대 크기 지정

typedef int element; //항목의 정의
typedef struct {
	element array[MAX_LIST_SIZE]; //배열 정의
	int size; //현재 리스트에 저장된 항목들의 개수
} ArrayListType;

 

<기초 연산>

//리스트 초기화 함수
void init(ArrayListType * L){
	L->size = 0;
}

//리스트가 비어있으면 1 아니면 0을 반환
int is_empty(ArrayListType * L){
	return L->size == 0;
}

//리스트가 가득 차 있으면 1을 반환 아니면 0을 반환
int is_full(ArrayListType * L){
	return L->size == MAX_LIST_SIZE;
}

//리스트 출력
void print_list(ArrayListType * L){
	for(int i = 0; i < L->size; i++)
    	printf("%d->", L->array[i]);
    printf("/n");
}

 

<항목 추가 연산>

//리스트 맨 끝에 항목을 추가하는 연산
void insert_last(ArrayListType * L){
	if(L->size >= MAX_LIST_SIZE){
    	printf("리스트가 찼습니다");
    }
    L->array[L->size++] = item;
}

//리스트 중간에 항목을 추가하는 연산
void insert(ArrayListType * L){
	if(!is_full(L) && (pos >= 0) && (pos <= L->size)){
    	for(int i = (L->size - 1); i >= pos; i--)
        	L->array[i+1] = L->array[i];
        L->array[pos] = item;
        L->size++;
    }
}

 

<항목 삭제 연산>

//특정 위치의 항목을 삭제하는 연산
element delete(ArrayListType * L, int pos){
	element item;
    
    if(pos < 0 || pos >= L->size){
    	printf("위치가 알맞지 않습니다");
    }
    item = L->array[pos];
    for(int i = 0; i < (L->size -1); i++)
    	L->array[i] = L->array[i+1];
    L->size--;
    return item;
}

 

<실행 시간 분석>

인덱스를 사용하여 항목에 바로 접근할 수 있으므로 속도는 O(1)이다. 삽입이나 삭제 연산은 다른 항목들을 이동하는 경우가 많으므로 최악의 경우는 O(n)이 될 수 있다. 맨 끝에 삽입하는 경우는 O(1)이 될 수 있다.

 

3. 연결 리스트

<연결리스트>

동적으로 크기가 변할 수 있고 삭제나 삽입 시에 데이터를 이동할 필요가 없는 리스트, 리스트의 구현에만 사용되는 것이 아닌 다른 여러가지 자료구조(트리, 그래프, 스택, 큐) 등을 구현하는데도 많이 사용된다.

 

위 사진에서 알 수 있다시피 줄로 연결된 상자라고 생각할 수 있다.

 

<연결리스트의 구조>

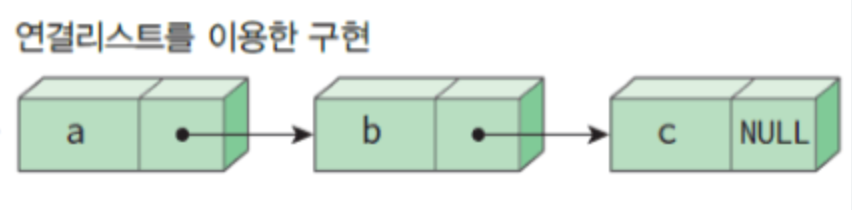
두개의 상자를 컴퓨터 용어로 (Node)라고 부른다. 연결 리스트는 이 노드의 집합이다. 노드들은 메모리의 어떤 위치에나 있을 수 있으며 다른 노드로 가기 위해서는 현재 노드가 가지고 있는 포인터를 이용할 수 있다.

 

노드는 데이터 필드(사진상으로 a가 있는)와 링크 필드(link field)가 존재한다. 

데이터 필드의 경우 우리가 저장하고 싶은 데이터가 들어가며, 링크 필드에는 다음 노드의 주소가 들어간다. 

 

연결리스트에 접근하기 위해서는 첫 노드를 알아야 전체 노드에 접근할 수 있다. 때문에 첫 노드를 가리키고 있는 변수가 필요한다 이를 

헤드포인터(head pointer) 라고하며, 마지막 노드는 가리킬 다음 노드가 없으므로 마지막 노드의 링크필드에는 NULL이 들어간다.

 

<연결리스트의 종류>

• 단순 연결리스트 체인이라고도 하며 마지막 노드의 링크가 NULL값을 가짐
• 원형 연결리스트 단순 연결리스트와 같으나 마지막 노드가 첫 노드를 가리킴
• 이중 연결리스트  각 노드마다 두개의 링크가 존재하며, 하나의 링크는 앞 노드를 다른 하나의 링크는 뒤의 노드를 가리킴